[LeetCode] Fibonacci Number
https://leetcode.com/problems/fibonacci-number/
The Fibonacci numbers, commonly denoted F(n) form a sequence, called the Fibonacci sequence,
such that each number is the sum of the two preceding ones, starting from 0 and 1. That is,
F(0) = 0, F(1) = 1
F(n) = F(n - 1) + F(n - 2), for n > 1.
Given n, calculate F(n).
Example 1:
Input: n = 2
Output: 1
Explanation: F(2) = F(1) + F(0) = 1 + 0 = 1.
Example 2:
Input: n = 3
Output: 2
Explanation: F(3) = F(2) + F(1) = 1 + 1 = 2.
Example 3:
Input: n = 4
Output: 3
Explanation: F(4) = F(3) + F(2) = 2 + 1 = 3.
Constraints:
0 <= n <= 30
피보나치 수열의 합을 구하는 문제.
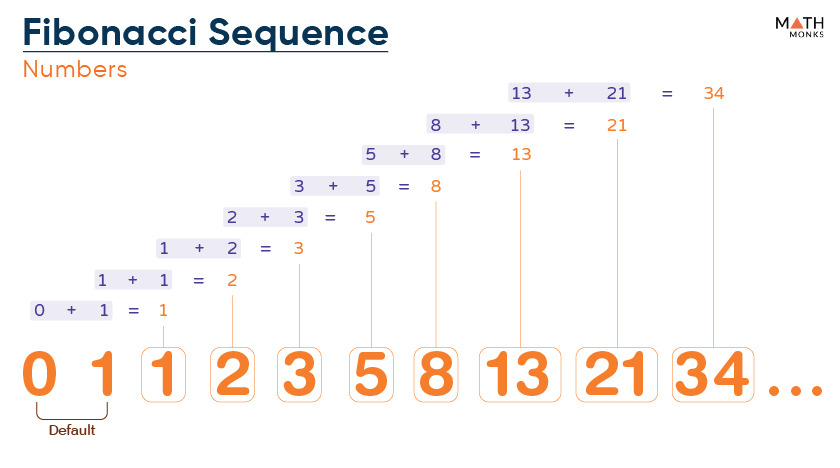
엄청 오랜만에 보는데.. 피보나치 수열은 아무튼 이런 것.
여태까지 했던 거에 비하면 굉장히 쉬울 거라고 생각했는데...
생각보다 쉽지가 않았다ㅋㅋㅋ 재귀함수에 입문하는 문제인데도...
/**
* @param {number} n
* @return {number}
*/
var fib = function(n) {
// F(n) = F(n-1) + F(n-2)
// F(0) = 0, F(1) = 1
// F(2) = F(1) + F(0) = 1
// F(3) = F(2) + F(1) = F(1) + F(0) + F(1) = 1 + 0 + 1 = 2
// F(4) = F(3) + F(2) = F(2) + F(1) + F(1) + F(0) = 1 + 1 + 0 + 1 + 0 = 3
// F(5) = F(4) + F(3) = F(3) + F(2) + F(2) + F(1) = 2 + 1 + 1 + 0 = 4
// F(6) = F(5) + F(4) = F(4) + F(3) + F(3) + F(2) = 3 + 2 + 2 + 1 = 8
const f = (n) => {
if(n==0){
return 0;
}
if(n==1){
return 1;
}
return f(n-1) + f(n-2);
}
return f(n);
};
어떻게 어떻게 풀어내긴 했으나 아니나 다를까 엄청나게 비효율적이다ㅋㅋㅋ
이건 그냥 n이 커질수록 O2^n 복잡도를 갖게 되기 때문에...ㅎㅎ
효율을 개선하는 방법은 두 가지 정도 있다.
1. 이전 값 기억하기 + 재귀함수
하나는 재귀함수를 이용하되 이전 계산값을 보관하는 걸로,
아래처럼 배열에 인덱스 n에 fib(n)을 저장하는 방식이 있을 수 있고.. (꼭 배열이 아니어도 되지만)
/**
* @param {number} n
* @return {number}
*/
var fib = function(n) {
const memo = [];
const f = (n) => {
if(n==0){
return 0;
}
if(n==1){
return 1;
}
if(memo[n]){
return memo[n];
}
let res = f(n-1) + f(n-2);
memo[n] = res;
return res;
}
return f(n);
};
2. DP
두 번째는... 동적 계획법이라고 하는 Dynamic Programming을 활용한 방식이다.
하나의 큰 문제를 여러 개의 작은 문제로 나누고 그 결과를 저장해서 재사용한다.

Richard Bellman이라는 수학자가 처음 고안했다고 한다.
그냥 일반적인 반복문이지만 재귀함수를 사용하는 것과 로직이 비슷하다.
단, 재귀함수는 일반적으로 큰 문제에서 작은 문제 방향로 접근하고, DP는 작은 문제에서 큰 문제로 접근한다는 차이점이 있다.
이것도 결국 이전 값을 보관하는 방법 중 하나인 것 같은데,
이 문제의 경우 prev와 curr, 그리고 next로 3개의 히스토리를 관리하면서 해결할 수 있고, DP를 쓰는 게 가장 효율적이다.
/**
* @param {number} n
* @return {number}
*/
var fib = function(n) {
if(n==0){
return 0;
}
if(n==1){
return 1;
}
let prev = 0; // fib(0)
let curr = 1; // fib(1)
for(let i=2; i<=n; i++){
const next = prev + curr;
prev = curr;
curr = next;
}
return curr;
};
이 경우에는 i가 0부터 시작할 필요가 없다.
prev와 curr의 초기값에서 이미 i가 0일 때와 1일 때를 보관하고 있기 때문이다.
n이 5일 때를 예로 들면 아래와 같이 반복문이 진행되면서 값을 바꿔 준다.
| i | prev = f(i-2) | curr = f(i-1) | next = f(i) |
| 2 | f(0) = 0 | f(1) = 1 | f(2) = 0 + 1 = 1 |
| 3 | f(1) = 1 | f(2) = 1 | f(3) = 1 + 1 = 2 |
| 4 | f(2) = 1 | f(3) = 2 | f(4) = 2 + 1 = 3 |
| 5 | f(3) = 2 | f(4) = 3 | f(5) = 3 + 2 = 5 |
i가 n이 될 때 f(n)의 결과가 curr에 저장되기 때문에 반복문의 조건도 i<=n인 것이다.
(조금만 로직을 수정해 주면 i<n도 물론 가능함)
얼레벌레 DP까지 맛보기 해버렸다~
DP 관련 참고 링크
'CodingTest' 카테고리의 다른 글
| [LeetCode] N-th Tribonacci Number (0) | 2025.05.21 |
|---|---|
| [LeetCode] Path Sum III (0) | 2025.05.19 |
| [LeetCode] Count Good Nodes in Binary Tree (0) | 2025.05.15 |





